z-scores

A common measure of dispersion is standard deviation, which gives an indication of the spread of the data. The concept of a standard score is based on the standard deviation. In particular, for any number it specifies how many standard deviations that number is away from the mean. It is found by subtracting the mean from the raw score, and then dividing the result by the standard deviation. When a data distribution is normally distributed, a standard score is known as a z-score:

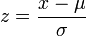
where μ is the mean and σ is the standard deviation.

z-scores are useful for calculating probabilities. In particular, probabilities can be calculated by computing the area under the normal curve for a given range. Practically speaking, there are several ways to go about this:

• The old way is to use a lookup table, which converts a z-score to an "area under the normal curve" number. These area under the normal curve numbers can be added and subtracted to get probabilities for a given interval.
• The fancy way is to use a little calculus to integrate the area under a normal curve.
• The modern way is to use a computer (like the online calculator below) to do the computation for you.

All of these techniques allows you to answer questions like "what is the probability of obtaining a score between X and Y?".

Example

Psychometrics tests are often standardized such that the scores form a normal distribution with a mean of 100 and a standard deviation of 15. Let's imagine that you take a test that measures your ability to solve crossword puzzles, and you get a score of 130. Obviously, that means you are pretty good at crossword puzzles. However, the question is: how good?

The first step is to compute the z-score: (130-100)/15 = 2. That means your score is 2 standard deviations above the average. The next step is to convert this into a probability. We could use a table of z-scores, and we would find that the area under a normal curve with z-scores less than a 2 is 97.7%. Saying "I am better than 97.7% of the population" is a lot more meaningful than "I got a score of 130".

The calculator below can also be used to calculate this figure. First enter the mean and standard deviation, and click "Submit". Second, move your mouse to the far left of the graph, and click once. Finally, move the mouse as close as you can to the raw score of 130, and click again. If all went well, you should get an answer pretty close to 97.7%.