Student's t-distribution

Student's t-distribution is a family of distributions that have a similar appearance as the normal distribution. However, the t-distribution is used when the real standard deviation of a population is unknown, and the standard deviation of a sample is used in its place. The degrees of freedom (df) of the t-distribution accounts for the increased uncertainty as a result of using an estimate of the standard deviation instead of the real parameter. This leads to a distribution that is more "spread out" than the normal distribution. As the degrees of freedom increases, the t-distribution approaches the normal distribution.

Estimating the population mean from a sample

Assume that we would like to know the average (mean) anxiety level that Canadian adults experience before public speaking. The only way to find the true mean would be to test every Canadian adult. Since this isn't possible, we perform a test using a small subset of the population (the sample), and use the results to infer a likely value or range of values for the true mean. We conduct the following experiment:

1. We select 10 random Canadian adults to participate in the study.
2. Each participant is given a task that involves public speaking, and before starting they rate their anxiety on a scale from 1 to 10.
3. Assume we get the following scores:  2, 5, 3, 7, 6, 7, 5, 3, 5, 3
4. We calculate the mean of our sample set: 4.6. This is known as the sample mean.

Is 4.6 likely to be a good estimate for the mean of the whole population of Canadian adults? Intuitively, the answer depends on the variance observed in our sample data and the number of participants in our experiment. More formally, we can use the one-sample t-test to test the hypothesis that the true value of the population mean is in a specified range.

The t-distribution

The t-distribution is at the heart of several important statistical tests. This is because some common test statistics follow a t-distribution. For example, consider the test statistic for the one-sample t-test:

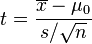
where x̄ is the sample mean, μ₀ is the hypothesized mean, s is the sample standard deviation, and n is the sample size. The sampling distribution of t-value is the t-distribution with n-1 degrees of freedom. Note that we are using the sample standard deviation instead of the true standard deviation; this is the reason the test statistic follows a t-distribution rather than a normal distribution.

As with z-scores, t-values are standardized so they can be used to compute probability values.